The Genetic Architecture of Complex Traits in Heterogeneous Stock MiceCan't be bothered with the background? Then just click here! Updated August 2008 - eQTL Data and Build 37 MappingThe BackgroundThe laboratory mouse is a key model organism for understanding gene function in mammals. The production of novel, highly penetrant mutations that can either be targeted to a gene of interest or introduced randomly in the genome by mutagenesis, are well established techniques for this purpose. However many aspects of gene function only become apparent from the analysis of low penetrance mutations, whose effects are not always related to those of the fully penetrant allele. Naturally occurring genetic variants are a source of low penetrance mutations. They explain, in part, why inbred strains of mice differ in so many ways: in physical and behavioural characteristics, in susceptibility to infection or to developing cancer. Because they give rise to quantitative variation they are often called quantitative trait loci or QTLs. The effect of each QTL is usually small, and this is one reason they are notoriously difficult to identify at a molecular level. Despite new genomic resources, such as access to dense maps of sequence variation, and the ability to interrogate the expression levels of virtually every gene, molecular dissection of QTLs remains a challenge. Yet, if we could find the genes they act upon, we would have a way of understanding the biology of many phenotypes of medical importance, such as weight, high blood pressure, anxiety and depression. One obstacle to progress is the difficulty in resolving QTLs into sufficiently small intervals to make gene identification possible. The classical approach begins by genetic mapping in a cross between two inbred strains and eventually results in the identification of a small number of independently segregating loci mapped into intervals larger than 20 megabases. Subsequent fine-mapping typically proceeds by repeatedly backcrossing one inbred strain onto another to isolate each locus. Such attempts are frequently frustrated when it is discovered that a single QTL segregating in inbred crosses fractionates into multiple smaller effects, each of which typically contributes much less than 5% to the total phenotypic variance. We have developed alternative methods for fine-mapping small-effect QTL that use outbred mice of known ancestry. We use a genetically heterogeneous stock (HS) of mice descended from eight inbred progenitor strains. Because the stock has been maintained for more than 50 generations, each chromosome is a fine-grained mosaic of the progenitor strains: the average distance between recombinants is small (less than 2 centimorgans) so that the HS provide high resolution mapping of multiple QTLs across the genome. This picture illustrates what happens during the construction of the stock. It shows one chromosome pair from each of the inbred strains above one chromosome pair from an HS mouse. Each inbred strain is shown in a different colour. You can see that the HS chromosome is a mosaic of its progenitors.
On this site we provide information about the stock and about an experiment we carried out to map QTLs that contribute to variation in over 100 traits, including models of human disease (asthma, type 2 diabetes mellitus, obesity and anxiety) as well as immunological, biochemical and haemotological phenotypes. You can browse the results, download the phenotypes and genotypes and, through the links we provide, obtain information about the genes that are present underneath the QTL peaks. However, in order to understand our results, and thereby use our data effectively, we encourage you to read the description of the methods we employed. In particular, it is important to understand how we report the significance of our findings, since we use a metric with which you may not be familiar: a Resample-based Model Inclusion Probability (RMIP). The MiceThe HS mice we used are derived from the following eight inbred strains: A/J, AKR/J, BALB/cJ, C3H/HeJ, C57BL/6J, CBA/J, DBA/2J and LP/J The progenitors were crossed to produce a genetically heterogeneous, and prolific stock.
The stock was originally created by Dr Robert Hitzemann in the 1980s and is currently maintained in his laboratory at the Department of Behavioral Neuroscience in the Oregon Health & Science University We set up a colony using 40 mating pairs to generate offspring for testing. Over a three year period, from 2002 to 2005, we tested more than 2,000 HS mice. We tested the eight progenitors on the same protocol, using 12 mice of each strain. There were 84 HS pedigrees, eight of which were large complex multi-generational families with inbreeding loops, encompassing the majority (61.1%) of individuals. The remaining 76 families were nuclear, with an average sibship size of 9.6 (range 2-34). The pedigrees consisted of over 4,000 potentially informative meioses, of which the average number of informative meioses per marker was 1,296.7 (range: 9-2,755 per marker), and the average number of phase-known meioses was 198.1 (range: 7-964 per marker). The PhenotypesOur intention is to analyse phenotypes of importance to human health. We targeted three diseases: anxiety, type II diabetes and asthma. These are all common and disabling conditions for which we currently have relatively ineffective treatments. We aimed also to collect as broad a range of measures as possible. We have information about each animal's respiratory physiology, its metabolism, as well as how it learnt and remembered a behavioural task. We obtained biochemistry, haematology and immunology profiles of each mouse. Collaborators are collecting data on bone density and morphology. Over time, we anticipate that additional phenotypes will be added to our database of results. This table provides a summary of the phenotypes we collected and for which we have mapping information. A full description has been published Solberg LC, Valdar W, Gauguier D, Nunez G, Taylor A, Burnett S, Arboledas-Hita C, Hernandez-Pliego P, Davidson S, Burns P, Bhattacharya S, Hough T, Higgs D, Klenerman P, Cookson WO, Zhang Y, Deacon RM, Rawlins JN, Mott R, Flint J. (2006) A protocol for high-throughput phenotyping, suitable for quantitative trait analysis in mice. Mamm Genome. 17(2) :129-46. and a PDF is available here
The GenotypesWe selected single nucleotide polymorphisms (SNPS) across the genome that distinguish between the eight HS founders. We used datasets to select SNPs that are validated and polymorphic in at least some of the HS founders. The SNPs were mapped onto the mouse genome and those closer than 50kb with identical strain distribution patterns were discarded. All gaps without SNPs over 500kb were filled using SNPs from Celera, Affymetrix SNPs and from the CZECHII mouse. The genotyping was carried out at Illumina (San Diego, CA) using their proprietary BeadArray genotyping platform. The SNP selection process provided 15,348 SNPs, including 120 unmapped SNPs at the time of the selection (build 33). The average interval between the selected SNPs based on build 34 is 167.0 Kb (SD=141.5). 99.0% of the intervals are below 500Kb and 81.2% below 250Kb. We obtained genotypes for 13,459 SNPs on 1,904 fully phenotyped mice and 298 parents, with an average of 13,441 genotypes per animal. The estimated accuracy of the genotypes is 99.99% based on the inheritance of alleles in 1,097 trios and 25 samples genotyped twice. 12,534 SNPs were polymorphic in the founder strains and 11,558 were heterozygous in the HS population, indicating that since the inception of the HS 7.8% of markers have drifted to fixation. The mean minor allele frequency was 30.5% in the founders and 26.7% in the HS. The mean interval between markers was 204.4 Kb, (s.d. 231.2 Kb) and 92.5% of the genome is within 500 Kb of a SNP. However, five intervals are larger than 3 Mb of which the largest (11.3Mb) is on the X chromosome. The genotypes can be downloaded here. The data are formatted for analysis by the HAPPY package, as pairs of chromosome-specific text files. E.g. chr1.build34.data, chr1.build34.alleles. The "data" files are in ped-file format and contain the genotypes. The "alleles" files contain the marker information. An explanation of the format may be found here. The Genetic MapWe constructed a new genetic map for the mouse, using the SNP data. This is the first high resolution map of the mouse genome to be created using SNPs and will be an essential resource for genetic mapping experiments. A full description of the map and how it was created is in Shifman et al, 2006 PlosBiology 4(12) e395 . We provide the following maps (these are identical to those on the PlosBiology web site as supplemental data): The AnalysisThe family structure in our sample causes genotype correlations (or linkage disequilibrium (LD)) that inflate QTL effects and complicate the interpretation of QTL mapping results: the effect at one QTL could be attributable to the effect at a second locus, possibly on a different chromosome. Genotype correlations can also result in one QTL becoming non-significant given the presence of a second, correlated, effect, even if both are genuine. Therefore we need to consider the joint effects of QTLs, and to identify a set of QTLs that act independently to explain the phenotypic variation. To deal with these issues we used model-averaging techniques. There are many possible multiple-QTL models built from the candidate QTLs found in the genome scans that can explain the data. So far we have considered only models built from autosomal additive QTLs identified in the genome scans. We created multiple datasets of 2,000 mice for analysis by randomly selecting animals from the genuine dataset. We sampled with replacement so that some animals are re-sampled several times and others not at all. For each of these bootstrap datasets, we constructed a multiple QTL model iteratively by forward selection. Starting with a model with no QTLs, the effect of adding a candidate QTL was tested. The QTL with the most significant improvement in fit was added to the model, provided the improvement exceeded a 5% genome-wide significance threshold. The procedure was repeated until no more significant QTLs could be added. We then averaged across all models. We scored each QTL by its Resample-based Model Inclusion Probability (RMIP), the proportion of bootstraps in which it was selected and estimated its apparent effect size after first removing variance attributed to covariates (such as sex and age). The apparent effect size is defined as the percentage variance explained by a given QTL after allowing for the other QTLs in the model, averaged across all models containing that QTL. Unfortunately simply knowing a RMIP does not immediately provide us with the likelihood that a QTL is genuine. The interpretation of a RMIP depends on the experiment from which it was derived. We have to calibrate RMIPs and we do so by simulation. In our case, since we found an average of seven QTLs per model, for each simulation we selected seven SNPs at random across the genome as true QTL locations. Then, without altering the genotypes or family structure, we simulated QTLs at these SNPs, each with an effect size explaining 5% of the phenotypic variance. A simulated 5% effect corresponds to an apparent 3% effect in the HS, typical of the apparent effect sizes we obtained in the genome scans. To investigate false positive rates we simulated a null QTL scenario which consisted solely of 35% family and 20% environment effects, under the assumption that there are no detectable QTLs, but that the genetic effect is due to independent genes of infinitesimally small effect. The table below shows the results of the simulations and provides performance measures for RMIP thresholds between 0.05 and 1. Each row collates the results for all peaks detected in the model averaging with RMIP exceeding the given threshold. We report three measures: first, the proportion of QTLs detected after model averaging that exceed a given RMIP threshold and match a true QTL; second, the proportion of true QTLs that are detected (this figure estimates power); third, the expected number of false positive QTLs detected per genome scan under the null QTL scenario. We see that over a wide range of RMIP values, the power to detect a QTL is about 90%. Furthermore, a QTL that exceeds a RMIP threshold of 0.5 will be true in 85% of cases, and in 70% of cases for a threshold of 0.25. Finally, under the assumptions of the simulations consisting solely of infinitesimal genetic effects, at a RMIP threshold of 0.25, about one false positive QTL occurs every 4 genome scans. This value can be thought of as the upper limit of the number of false positive QTLs under an infinitesimal genetic model.
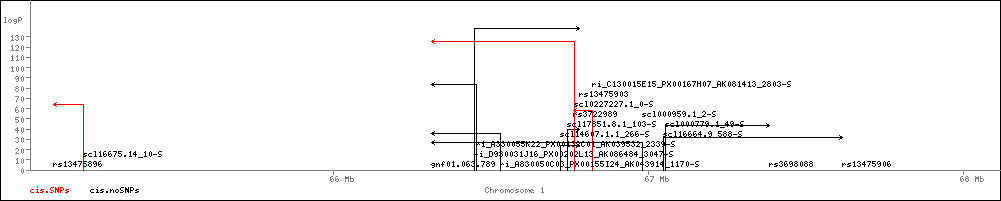
NOTE The data in the Table are based on 100 simulation trials. In each trial, seven 5% QTLs were simulated and mapped. The fourth Column gives the proportion of the seven that were detected at a given RMIP threshold. For example, at RMIP=0.05 most simulations found 6 of them. However, it is not possible to infer the total number of QTLs from this table, for two reasons. First, because the fourth column does not refer to all QTLs (only those with efffect size exceeding 5%), and second, because it is not possible to infer the total number of QTLs, which is a meaningless quantity unless parameterized by the size of the effect. Consider a model of QTL action in which a large number of QTLs influence the trait with effect sizes distributed according to a exponential-like distribution in which there are a few major players (eg, >5% QTLs) and 1000s of minor actors (less than 1% QTLs). Suppose there are seven 5% QTLs and one thousand 0.001% QTLs. If we found all seven 5% QTLs that would be a pretty good result. Yet, if the power in the fourth colum were based on the total number of QTLs then the proportion would be 7/1007= ~0.007. Moreover, under an infinitesimal model the number in the fourth column would always be 0 regardless of how successful we were. Therefore, for the power column to be meaningful in any sense its definition is constrained to refer to 5% QTLs. That is reasonable a priori since 5% is a typical effect size seen in reported QTLs (Flint et al, NRG, 2005), though a posteriori we might conject 2-3% is more common in our study. Note the above means that column three, also based on these simulations, is conservative because whereas dropping to low RMIPs is unlikely to yeild many more 5% QTLs it will pick up more QTLs of smaller effect. Mapping eQTLsNatural genetic variation contributes significantly to variation in gene expression and the loci of regulatory variation for individual transcripts have been mapped using both genetic linkage and association methodologies in a number of organisms. These studies show that variation in transcript abundance arises from expression quantitative trait loci (eQTL) that can be classified as either local (cis-eQTLs) or distant (trans-eQTLs) regulatory variants. Typically multiple eQTLs contribute to variation in the abundance of a single transcript. We used an Illumina array with 47,430 oligonucleotides to assess expression of 21,288 Ensembl annotated transcripts, representing 19,687 genes. We analysed mRNA extracted from the hippocampus of 460 HS animals, and the livers and lungs of 260. Genome scans were performed to map the eQTLs for all transcripts and tissues on to build 37 of the mouse genome. eQTLs were categorized as either cis or trans depending on whether an eQTL peak was either less or more than 2 Mb from the mid point of its cognate transcript (in the HS the linkage disequilibrium measured by the mean r2 falls to less than 0.5 within 2 megabases and is less than 0.2 within 8 Mb). The number of eQTLs detected depends on the RMIP threshold applied. In the hippocampus, at the most stringent RMIP value of 1.0, we detected 2,732 cis-eQTLs and 205 trans eQTLs; at the lower RMIP value of 0.25 there are 3,961 cis-eQTLs and 4,586 trans eQTLs. It is important to appreciate that while the RMIP measures the robustness of the eQTL detection, it is not a measure of the effect size of the eQTL. This is shown by the lack of correlation between RMIP and either the ANOVA logP or the percentage of variance explained (which do correlate). We have now incorporated the cis-eQTL results into gscandb so that it is possible to see which genes at a QTL are likely candidates. We faced a number of difficulties in presenting the data. First, because there are so many loci, it would be impossible to show individual scans for all 20,000 or so transcripts. We decided to show only the cis-effects, indicating the peak of the logP by an arrow, whose shaft is placed in the cognate gene. In this way we are able to show all cis-eQTLs in one track. To see this track you must do two things: first, enable the "cis.SNPs" and/or "cis.noSNPs" in the Scan Types box on the right of the screen. Second, choose one or more tissues from the list of Plottable Scans. There are currently three to choose from: eQTL.Lung, eQTL.liver and eQTL.hippocampus.The example below shows cis eQTLs for the Hippocampus on part of chromosome 1.
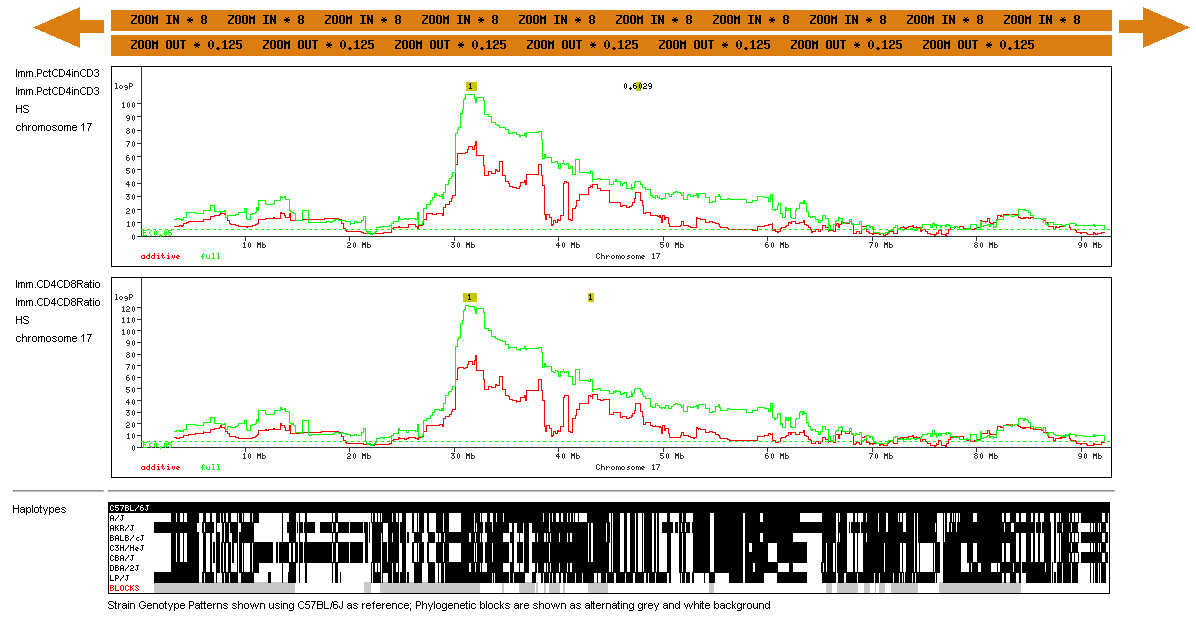
Second, we found that among cis-eQTLs with a logP greater than 20, about 40% contain a known polymorphism in the target sequence; we estimate that a further 10% are associated with unannotated SNPs. Therefore we felt it was imperative to indicate which cis-eQTLs might be false positives due to the presence of SNPs. We have used colour to distinguish those eQTLs that have SNPs (red) from those that do not (black). The two displays are chosen by enabling the "cis.SNPs" and/or "cis.noSNPs" in the Scan Types box What the Genome Scans Look LikeThe example below shows the region view for two immunology phenotypes, CD4/CD8 ratio and CD4:CD3 over the mouse MHC on chromosome 17. |
|
The chromosome is displayed along the horizontal axis. There are 6 vertical components to the display:
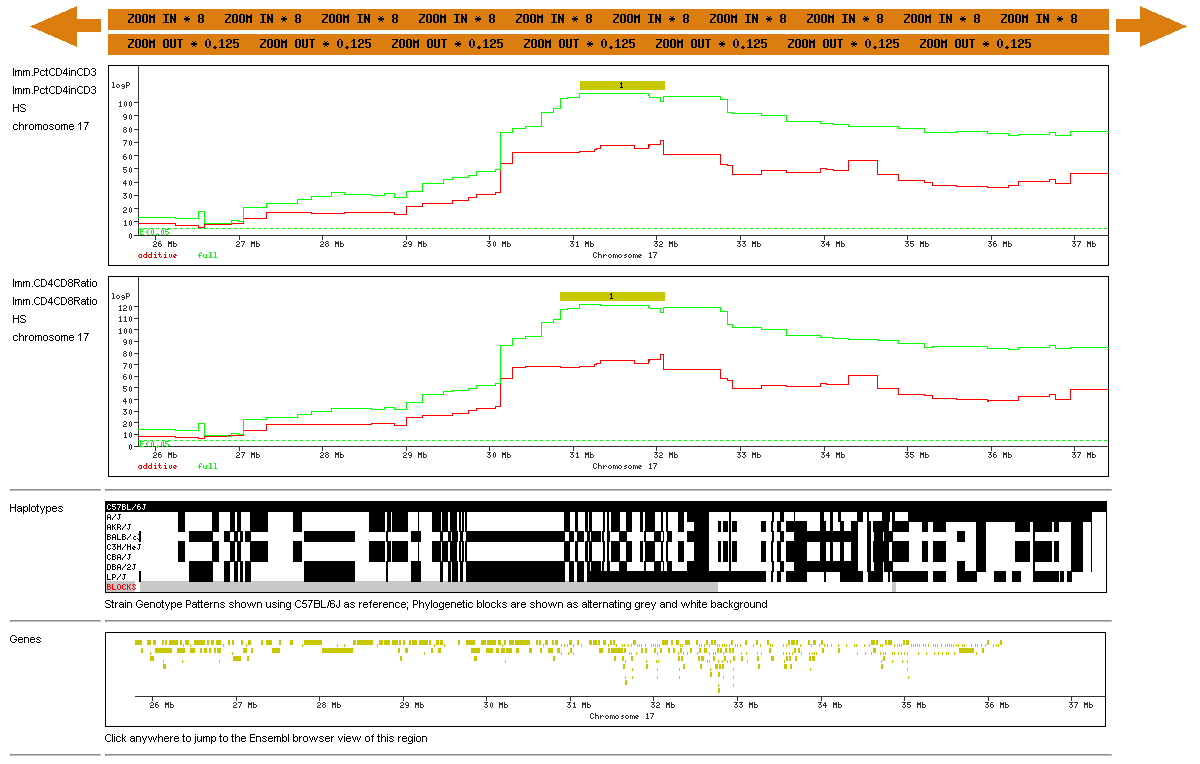
The effect of zooming in on one of the phenotypes (CD4) is shown below: |
|
The genome scans are now redrawn at higher resolution. The black QTL feature is now much larger. The genes are now shown with more accurate lengths. Zooming in once more will produce a even more detailed view with the names of genotypes SNPs shown, gene names displayed, and a list of gene annotations with links to other genome databases (the gene list is truncated in the example shown below): |

Build37 MappingWe have completely remapped all phenotypes to the latest build of the mouse genome, using the same model averaging based approach, but with some significant changes. Perhaps the most important of these for the users of our data is the way we now report the locations of QTLs. In association mapping of highly recombinant populations that have confounding long-range genetic correlations (such as the HS), the bootstrap approach that we originally used is problematic. If there are two association peaks A and B on the same chromosome, estimating the bootstrap confidence interval of A means first specifying a range of markers to be rescanned that could not pick up an association signal from B but at the same time is broad enough to capture variability of A. Defining this range thus requires estimating the likely variability in the location of peak A and B beforehand, a circular problem which it is not possible to resolve. In fact, to the put difficulty more generally, we believe that in mapping multiple small effects for complex traits, the inevitable outcome of detecting multiple closely linked associations will often defy a meaningful definition of a confidence interval. A modification of our model averaging method allows one solution to this problem. In our published method for analyzing an HS using model averaging, we did not allow all possible genetic predictors in the model. Rather we performed model selection on distantly spaced marker intervals that each represented the apex of an association peak above the genomewide significance threshold. However in our new analyses we incorporate all markers and, by so doing, the resampling method provides a consistent framework for characterizing the variability in location of a QTL. During re-sampling, we determine the proportion of times at least one marker is included in a model. Because this proportion is based on fitting many multilocus models, it automatically takes into account the effect of confounding signals from elsewhere in the genome. Locus identification is based on the frequency with which it recurs in the re-sampling. The new approach does not provide a confidence interval for a particular causal variant. Rather, it provides the inclusion probabilities for each interval. We have therefore included these with each scan. You can see the inclusion probabilities for any phenotype by choosing the relevant .RMIP file from the list of plottable scans. Note that the orange bar showing the QTL interval does NOT show a 95% confidence interval. Instead it shows a region of near continuous inclusion probabilities greater than zero, and the number contained in the bar is the summation of those probabilities. Finally, the phenotype names in the new database are not the same as in the old. To make life easier for ourselves we have kept the names used in the database files. These conform to the requirements of the analysis package (R), but are not as immediately clear as the ones we had originally made available. Therefore we provide here a simple look up table to make the meaning of the phenotype names transparent. In the table EPM refers to the elevated plus maze, IPGTT to the intraperitoneal glucose tolerance test, FN to food neophobia, FPS to fear potentiated startle and OFT to the open field test.
What the Data Look LikeWe describe here the format of the data that you can download. If you want to look at the results, click on gscandb Naming conventionsMost mice were microchipped and are named by their barcode, eg A048005080. The exceptions are some HS parents that are named according to cage, eg H2.3:G2.2(3). Mouse families are defined at the level of sibship, and named as "Mother Father". QTLs are mapped to marker intervals, not points. Each marker interval is about 200kb wide on average and is named by the id of the left-hand or proximal marker. The name of the right-hand marker can be determined easily from the genetic or physical map. Phenotype DataEach phenotype file always contains a column SUBJECT.NAME, followed by other columns containing phenotype measures (e.g. EMO in this example) and folowed by covariates such as GENDER, Family (defined as sibship, and labelled by the names of the parents), Date.StudyDay etc. Related phenotypes (e.g. all measures pertaining to a particular test) are in the same file. Within each phenotype file only those covariates with a statistically significant association with the phenotypes are included. Missing data are labelled NA. The Phenotypes are given as tab-delimited text files with a header, eg. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
The phenotypes measured include:
Genotype DataThe Genotypes are given as chromosome-specific text files. Each chromosome is described as a pair of files suitable for input into the R HAPPY package: a ped-format .data file that contains the HS genotypes and a HAPPY format .alleles file that contains the HS founder genotype information. Full file format details are available. Missing genotypes are coded as NA. the map is based on the build34 sequence map. Genome Scan DatabaseThe results of genome scans for 101 phenotypes are available from gscandb. The models used to fit each phenotype are given in the Model Menu, using the R language model syntax. Most phenotypes were fit using a linear model except for three latency phenotypes that were fitted using a survival modelling framework. Publications
Contact Richard Mott Jonathan Flint or William Valdar for more details. |